Description
题目链接: https://www.zhixincode.com/contest/12/problem/I?problem_id=191
题意是有一场 $n$ 个选手参加的石头剪刀布比赛,第 $i$ 个选手坐在第 $i$ 个位置,每个选手都有 $3$ 种可能情况
接下来有 $m$ 个询问,操作 $1$ $x$ $y$ 表示让 $y$ 位置的选手去挑战 $x$ 位置的选手,获胜的选手坐在 $x$ 位置,守擂方获胜概率为 $\frac{2}{3}$ ,攻擂方获胜概率为 $\frac{1}{3}$ ,操作 $2$ $x$ 表示询问初始位置为 $x$ 的选手仍未被淘汰的方案数
Solution
jls 所谓 very easy 的题目 QvQ
每个操作 $1$ 可以认为是 $y$ 向 $x$ 连一条有向边,其中攻擂方 $y$ 原先集合的所有元素的存活概率都乘上 $\frac{1}{3}$,而守擂方 $x$ 原先集合的所有元素的存活概率都乘上 $\frac{2}{3}$
每次查询的结果其实就是 $x$ 的存活概率乘上总的方案数 $3^n$
可以用带权并查集来实现这一过程
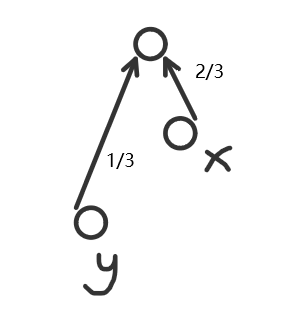
每次连边,都建一个新点,然后从 $y$ 连一条权值为 $\frac{1}{3}$ 的边,从 $x$ 连一条权值为 $\frac{2}{3}$ 的边
查询的过程等价于从结点 $x$ 向上走到当前根节点,答案就是路径上权值的乘积,路径可以在查询的过程中进行压缩
AC code
Time: 139ms
Memory: 8MB
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<bits/stdc++.h>
using namespace std;
#define mem(a,i) memset(a,i,sizeof(a))
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
#define lowbit(x) (x&-x)
#define pb push_back
#define fi first
#define se second
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
const ll mod=998244353ll;
const int maxn=4e5+5;
int n,m;
ll val[maxn];
int fa[maxn];
ll a,b;
int cnt;
ll qpow(ll a,ll x) {
ll res=1;
ll p=a;
while(x) {
if(x&1) res=res*p%mod;
p=p*p%mod;
x>>=1;
}
return res;
}
ll find(int x) {
if(fa[x]==x) return x;
else {
ll p=find(fa[x]);
val[x]=val[fa[x]]*val[x]%mod;
return fa[x]=p;
}
}
void connect(int x,int y) {
int p=++cnt;
int fa_x=find(x);
int fa_y=find(y);
val[fa_x]=a;
val[fa_y]=b;
fa[fa_x]=p;
fa[fa_y]=p;
}
int main() {
scanf("%d%d",&n,&m);
ll res=qpow(3ll,n);
a=qpow(3ll,mod-2);
b=a*2ll%mod;
rep(i,0,maxn-1) {
fa[i]=i;
val[i]=1;
}
cnt=n;
rep(i,1,m) {
int o;
scanf("%d",&o);
if(o==1) {
int x,y;
scanf("%d%d",&x,&y);
connect(y,x);
}
else {
int x;
scanf("%d",&x);
find(x);
ll ans=res*val[x]%mod;
printf("%lld\n",ans);
}
}
return 0;
}